Para estudar operadores lógicos vamos primeiro entender a teoria dos conjuntos. A propriedade que define o conjunto é serem alunos do ensino médio da Escola estadual “Bento de Abreu”. Os objetos do conjunto são os indivíduos do universo das pessoas que são alunos do ensino médio da Escola estadual “Bento de Abreu” e que por essa razão pertencem ao conjunto.
- E representa o conjunto de todos os alunos do ensino médio da Escola estadual “Bento de Abreu”, e E é o conjunto do universo de estudantes da Escola estadual “Bento de Abreu” que têm em comum a propriedade e de serem seus alunos do ensino médio.
- D representa o conjunto dos alunos da Escola estadual “Bento de Abreu” que têm em comum a propriedade D de lá estarem matriculados no curso técnico do SENAI "Henrique Lupo".
- B representa o conjunto dos aluno do curso técnico do SENAI "Henrique Lupo" que têm em comum a propriedade B de serem do curso Técnico em Eletroeletrônica.
- A representa o conjunto dos aluno do curso técnico do SENAI "Henrique Lupo" que têm em comum a propriedade A de serem do terceiro termo.
Como se pode verificar os elementos dos diversos conjuntos representados têm propriedades em comum, e há indivíduos que pelas suas características pertencem a vários conjuntos. Vamos então coloca-los nas devidas posições.
Percebido o conteúdo dos conjuntos com que vamos trabalhar e colocados todos na posição apropriada, chega agora a ocasião de entendermos como se define o relacionamento dos vários objetos do conjunto D conforme as suas propriedades.
Em lógica proposicional, a uma afirmação que pode assumir o estado de verdadeira ou falsa, chama-se proposição.
As afirmações contempladas numa proposição, podem até envolver fórmulas que exprimam relações entre várias afirmações estabelecidas com operadores lógicos, mas a sua resposta será sempre só uma de entre duas possíveis: verdadeira ou falsa. As proposições representam então, as fórmulas da lógica proposicional ou cálculo proposicional, representados pelos operadores lógicos.
Operador lógico AND
A análise de uma proposição através do operador lógico AND (E), ou conjunção lógica, resulta em um valor lógico verdadeiro se e somente se, todos as proposições que a compõem tiverem um valor verdadeiro.
- A empresa precisa de indicação para uma vaga de emprego (C) de alunos do terceiro termo (A) e do curso Técnico em Eletroeletrônica (B).
As expressões algébricas ou de lógica proposicional que representam este operador podem ser: a . b ⇔ a AND b.
E o símbolo da porta lógica que representa a análise destas duas proposições, agora como os operandos a e b com os valores 1 ou 0, devolvendo verdadeiro ou falso, agora como uma saída S com o valor 0 ou 1, é o representado na figura 1 ao centro.
A tabela verdade deste operador, representada na Figura 1 do lado direito, diz-nos o valor da saída S da porta lógica AND para os diversas combinações dos operandos a e b, confirmando aquilo que acabámos de constatar, i.e. que a resposta é verdadeira se e só se ambas as entradas forem verdadeiras.
Operador lógico OR
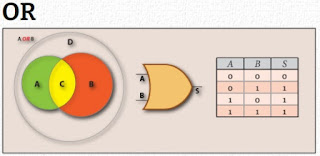
A análise de uma proposição através do operador lógico OR (OU) ou disjunção lógica, resulta em um valor falso se e só se, todos os operandos tiverem um valor falso.
- O aluno será indicado para uma vaga de emprego (C) se alunos estiver no terceiro termo (A) ou se for do curso Técnico em Eletroeletrônica (B).
E o símbolo da porta lógica que representa a análise destas duas proposições atómicas, agora como os operandos a e b com os valores 1 ou 0, devolvendo verdadeiro ou falso, agora como uma saída S com o valor 0 ou 1, é o representado na figura ao centro.
A tabela verdade deste operador, representada na figura 2 do lado direito, diz-nos o valor da saída S da porta lógica OR para os diversas combinações dos operandos a e b, confirmando aquilo que acabamos de constatar, que a resposta é falsa se e só se ambas as entradas forem falsas.
Operador lógico NOT
A análise de uma proposição pelo operador lógico NOT (NÃO) ou inversor lógico, resulta verdadeiro se a proposição em análise for falsa e vice-versa.
- O aluno do curso técnico em eletroeletrônica não será indicado para vagas com contrato de dois anos, se estiver no terceiro termo: /A = B
Podemos assim concluir que o operador NOT define a Diferença do conjunto A, como se pode ver no diagrama de Venn da figura 3. Este é o caso representado na figura, mas o mesmo se poderá dizer relativamente ao conjunto B.
As expressões algébricas ou de lógica proposicional que representam este operador podem ser: ¬A ⇔ NOT A.
O símbolo da porta lógica deste operador é o que está representado na figura 3 ao centro e a tabela verdade é a que está representada na mesma figura mas à direita.
Operador lógico XOR
- O aluno será indicado para uma vaga de estágio (C) se somente estiver no terceiro termo (A) ou se frequentar o curso Técnico em Eletroeletrônica (B).
Uma proposição analisada através de um operador XOR produz um valor verdadeiro quando, sendo uma das suas proposições atómicas verdadeira, a outra for falsa. eXclusive OR (OU exclusivo) significa precisamente sempre um dos dois mas nunca ambos. Operador diferença significa sempre diferentes, nunca coincidentes.
As expressões algébricas que representam este operador podem ser: a ⊕ b ou a XOR b
O símbolo da porta lógica e a Tabela verdade deste operador são os que estão representados na figura acima.
Operador lógico NAND
Uma proposição analisada através de um operador NAND produz um valor falso, se e só se, todas as suas proposições atómicas forem verdadeiros, ou seja, o NAND produz um valor verdadeiro se pelo menos uma das suas proposições atómicas for falsa.
- A empresa não precisa de indicação para uma vaga de emprego (C) de alunos que estão no terceiro termo (A) e são do curso Técnico em Eletroeletrônica (B).
Podemos então concluir que o operador NAND define a Diferença da Intersecção dos conjuntos A e B, pois define o conjunto dos objetos que não pertencem à sua intersecção, como se pode ver no diagrama de Venn da Figura 1.
As expressões algébricas ou de lógica proposicional que representam este operador podem ser: (a . b) ou a NAND b.
O símbolo da porta lógica e a Tabela verdade deste operador são os que estão representados na figura acima.
Operador lógico NOR
- O aluno não será indicado para uma vaga de emprego (D) se alunos estiver no terceiro termo (A) ou se for do curso Técnico em Eletroeletrônica (B).
Uma proposição analisada através de um operador NOR produz um valor verdadeiro, se e só se, todas as suas proposições atómicas forem falsas, ou seja, o NOR produz um valor falso se pelo menos uma das suas proposições atómicas for verdadeira.
Podemos então concluir que o operador NOR define a Diferença da União dos conjuntos A e B, pois define o conjunto dos objetos que não pertencem à sua União, como se pode ver no diagrama de Venn, além do símbolo da porta lógica e a tabela verdade deste operador estão representados na figura acima.
As expressões algébricas que representam este operador podem ser: a+b ou a NOR b ou NOT (a OR b).
Operador lógico XNOR
Uma proposição analisada através de um operador XNOR produz um valor verdadeiro quando as suas proposições atómicas são ambas verdadeiras ou são ambas falsas. Operador coincidência significa sempre coincidentes, nunca diferentes.
Podemos então concluir que o operador XNOR define a Identidade simétrica dos conjuntos A e B, conforme se pode ver pelo diagrama de Venn da figura acima.
As expressões algébricas que representam este operador podem ser: A ≡ B ou A XNOR B.
O símbolo da porta lógica e a Tabela verdade deste operador são os que estão representados na figura acima.
© Direitos de autor. 2020: Gomes; Sinésio Raimundo. Última atualização: 15/04/2020
Nenhum comentário:
Postar um comentário