Toda frase compreensível e que comunique alguma informação pode ser representada por meio de uma expressão algébrica booleana. A compreensão da lógica booleana aplicada à formulação de ideias e pensamentos facilita a capacidade de comunicação. O uso de transformações lógicas corretas permite que se coloque as palavras de modo a se obter a reação desejada em quem recebe a informação.
A habilidade no uso da lógica booleana aplicada à comunicação interpessoal é, particularmente, útil, necessária e largamente empregada em certas profissões, como, por exemplo: Professores; Pedagogos; Psicólogos; Políticos; Advogados; Vendedores; Oradores; Porta-vozes; Jornalistas; Escritores e Homens de negócios.
A introdução à lógica booleana é feita é feita na criança assim que ela inicia seu aprendizado na capacidade de comunicar-se.
As frases usadas como exemplo são meramente ilustrativas, não consistem de divulgação de mensagem explícita, nem subliminar, nem da opinião do autor sobre os diversos assuntos abordados. Exemplos são usados para que se evidencie a aplicação da lógica booleana na comunicação do dia-a-dia.
Entidades da lógica
- Variável lógica: Letra ou palavra para a qual se associa uma sentença.
- Sentença ou proposição: Frase que expõe um determinado acontecimento.
- Variável verdadeira: Sua afirmação é satisfeita. Valor verdadeiro: 1.
- Variável falsa: Sua afirmação não é satisfeita. Valor falso: 0.
- Não existe um terceiro valor.
- Uma variável somente pode ser verdadeira ou falsa.
Exemplos: A: Fazer sol; B: Chover; C: Ir trabalhar.
Unicidade da verdade
- Não existem duas verdades.
A verdade é uma só. Se duas proposições são mutuamente excludentes, uma delas é falsa e a outra é verdadeira, ou são ambas falsas.
Falácia das duas verdades I: Você já deve ter lido a respeito do caso onde uma pessoa lê o número 6 e a outra pessoa lê o número 9. Nesta estória, o leitor é induzido a acreditar que existem duas verdades, a depender do ponto de vista do analista. Isso é mentira.
Um dos dois observadores está lendo o número de cabeça para baixo, está fazendo uma interpretação errada. A pessoa que desenhou o número quis expressar 6 ou 9, 10 mas não ambos.
Falácia das duas verdades 2: Você já deve ter lido a respeito do caso onde uma pessoa enxerga um quadrado, e outra pessoa enxerga um círculo. Os dois observadores estão fazendo uma leitura errada, pois o cilindro não é nem um quadrado, nem um círculo.
Os dois estão fazendo uma interpretação bidimensional de uma figura tridimensional.
OPERAÇÕES LÓGICAS
Princípio do meio excluído: Não há um terceiro valor para a lógica booleana.
Conectivo: Operação que une duas ou mais sentenças. Para os matemáticos, os conectivos (lógicos e aritméticos) unem, apenas, duas variáveis ou constantes (entradas). Para os engenheiros, o conceito de conectivo é expandido para mais de duas entradas. Principais conectivos lógicos: E (AND), OU (OR), OU-Exclusivo (XOR), além da Negação (NOT).
NEGAÇÃO LÓGICA
Negação: Transforma o verdadeiro em falso e vice-versa.
Uma dupla negação não tem efeito. Veja os exemplos de negação lógica abaixo. - Afirmação: A = ir trabalhar
- Negação: /A = não ir trabalhar
Variáveis opostas: B = /A
- Se A é verdadeiro, então B é falso.
- Se A é falso, então B é verdadeiro.
- Se A=1, então B=0.
- Se A=0, então B=1.
Equivalências de negação: - Se você não trabalhar, passará fome: /A = B
- Você passará fome se não trabalhar: B = /A
- Se você trabalhar, não passará fome: A = /B
- Você não passará fome se trabalhar: /B = A
Sendo: A = Trabalhar e B = Passar fome.
- Uma dupla negação não tem efeito.
- Uma quantidade par de negações não tem efeito.
- Uma quantidade ímpar de negações pode ser representado por uma única negação.
MULTIPLICAÇÃO LÓGICA - AND de duas variáveis: C = A * B.
- A sentença é verdadeira se, e somente se, as duas variáveis forem verdadeiras.
- No contrário, a sentença é falsa.
- Se uma das variáveis de entrada for falsa, a variável de saída é falsa.
Exemplo 1: Eu vou ao cinema se, e somente se, eu tiver dinheiro e tiver um bom filme em cartaz. B = Ter bom filme em cartaz.
Exercício 1: O aluno é aprovado se tiver média superior a 6,0 e frequência superior a 75%.
Exercício 2: A implantação deste projeto requer tempo e dinheiro.
MULTIPLICAÇÃO LÓGICA - AND de três variáveis: D =A * B * C
- A sentença é verdadeira se, e somente se, as três variáveis forem verdadeiras.
- No contrário, a sentença é falsa.
- Se uma das variáveis de entrada for falsa, a variável de saída é falsa.
Exemplo 1: Eu vou passear se tiver companhia, se tiver um local legal para ir e se o tempo estiver bom, senão não.
D = Ir passear.
A = Ter boa companhia.
B = Houver um local legal.
C = O tempo estiver bom.
D = A * B * C
Exercício 1: Eu vou namorar alguém que tenha erudição, boa moral e boa aparência.
Exercício 2: Utopia capitalista: Bom, bonito e barato.
Exercício 3: Utopia socialista: Público, gratuito e de qualidade.
MULTIPLICAÇÃO LÓGICA - AND de quatro variáveis: E =A * B * C* D
Exemplo 1: Para ser contratado, o professor precisa ser aprovado na prova escrita, na prova didática, na prova de títulos e no exame médico.
E = Contratação.
A = Prova escrita.
B = Prova didática.
C = Prova de títulos.
D = Exame médico.
E = A * B * C* D
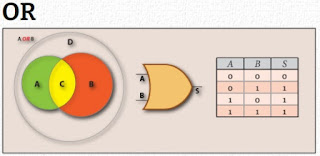
ADIÇÃO LÓGICA - OR de duas variáveis: C = A+ B
- A sentença é falsa se, e somente se, as duas variáveis forem falsas.
- No contrário, a sentença é verdadeira.
- Se uma das variáveis de entrada for verdadeira, a variável de saída é verdadeira.
Exemplo 1: Eu vou sair de casa se tiver que trabalhar ou se quiser passear.
C = Sair de casa.
A = Ir trabalhar.
B = Ir passear.
C = A + B
Exercício 1: A competitividade da empresa depende da qualidade de seu produto ou da deficiência da concorrência.
ADIÇÃO LÓGICA - OR de três variáveis: D = A + B + C
- A sentença é falsa se, e somente se, as três variáveis forem falsas.
- No contrário, a sentença é verdadeira.
- Se uma das variáveis de entrada for verdadeira, a variável de saída é verdadeira.
Exemplo 1: Eu quero um emprego que seja tranquilo, ou que pague bastante, ou que seja algo de que eu goste. D = Querer o emprego.
A = Ser tranquilo.
B = Oferecer bom pagamento.
C = Ser prazeroso.
D = A + B + C
Exercício 1: Eu vou te ajudar se eu tiver tempo, ou se você pagar, ou se eu tiver interesse nisso.
OU EXCLUSIVO - Só existe XOR de duas variáveis: C =A⊕ B
- As sentenças requerem exclusividade, um ou outro, mas não ambos.
- A sentença é verdadeira se uma e apenas uma das variáveis for verdadeira.
- A sentença é verdadeira se as duas variáveis forem diferentes.
- A sentença é falsa se as duas variáveis forem iguais.
Exemplo 1: Eu só quero trabalhar em Araraquara ou Piracicaba.
C = Querer o trabalho.
A = Em Araraquara.
B = Em Piracicaba.
C = A ⊕ B
Exercício 1: Vou comer o bolo de chocolate ou o de nozes, mas não aguento comer os dois.
Exercício 2: Hoje vou sair com a jaqueta de couro ou com a moletom.
Exercício 3: Vou ingerir uma bebida fermentada ou uma bebida destilada.
Exemplo 2: Para escrever, preciso de uma caneta ou um lápis.
C = Escrever.
B = Ter um lápis.
C =A + B
Para escrever, uso uma caneta ou um lápis.
C = Escrever.
A = Usar uma caneta.
B = Usar um lápis.
C = A ⊕ B
- É possível, para uma pessoa, precisar de uma caneta e de um lápis ao mesmo tempo, caracterizando, assim, um “OU inclusivo”.
- Não é possível, para uma pessoa, usar uma caneta e um lápis ao mesmo tempo, caracterizando, assim, um “OU” exclusivo.
- A determinação se o “OU” é inclusivo ou exclusivo depende da interpretação do texto. Nem sempre isso é fácil.
NAND - NAND de duas variáveis: C = /(A * B)
- A sentença é falsa se, e somente se, as duas variáveis forem verdadeiras.
- No contrário, a sentença é verdadeira.
- Se uma das variáveis de entrada for falsa, a variável de saída é verdadeira.
Exemplo 1: O aluno não é aprovado se o aluno perder a matéria e se for displicente nos estudos em casa. C = Ser aprovado.
A = Perder a matéria.
B = Ser displicente nos estudos em casa.
C = /(A * B)
Exercício 1: Eu não vou perdoar você se você fizer mal a mim e não pedir perdão.
NOR - NOR de duas variáveis: C = /(A + B)
- A sentença é verdadeira se, e somente se, as duas variáveis forem falsas.
- No contrário, a sentença é falsa.
- Se uma das variáveis de entrada for verdadeira, a variável de saída é falsa.
Exemplo 1: O aluno não entra na escola se estiver embriagado ou portando arma.
C = Entrar na escola.
A = Estar embriagado.
B = Portar arma.
C = /(A + B)
Exercício 1: O homem não se sente realizado se for trabalhar em um serviço imoral ou ilegal.
Exercício 2: O café não fica bom se estiver frio ou amargo.
Exercício 3: Seu cônjuge não mais te amará se você desrespeitá-lo ou se você desprezá-lo.
Exercício 4: Mãe para o filho: - Você não vai ao cinema se continuar fazendo bagunça ou se continuar batendo na sua irmãzinha.
Exercício 5: A economia de um país não funciona se o governo imprime dinheiro e se oferece crédito subsidiado.
Teoremas de De Morgan
Modo 1: A * B = /(/A + /B)
Exemplo: A implantação deste projeto requer tempo e dinheiro. C = Implantar o projeto.
A = Ter tempo.
B = Ter dinheiro.
C = A*B
Este projeto não pode ser implantado se não houver tempo ou se não houver dinheiro, ou ambos.
C = /(/A + /B).
Modo 2: A + B = /(/A * /B).
Exemplo: Eu vou sair de casa se tiver que trabalhar ou se quiser passear. C = Sair de casa.
A = Ir trabalhar.
B = Ir passear.
C = A + B
Eu não vou sair de casa se não tiver que trabalhar e se eu não for passear.
C = /(/A * /B).
Elemento idêntico da adição lógica
0 + 0 = 0
1 + 1 = 1
Exemplo 1: Para se formar, ou o aluno estuda, ou ele estuda.
B = O aluno formar-se.
A = O aluno estuda.
B = A+A.
B = A.
Para se formar, o aluno deve estudar.
Exercício 1: O escravo, ou obedece, ou obedece.
Elemento idêntico da multiplicação lógica
0*0=0
1*1=1
Exemplo 1: A criança chorava e chorava...
B: A sentença.
A = A criança chorar.
B = A*A.
B = A.
A criança chorava...
Exercício 1: Eu esperei você por horas e horas.
Exercício 2: Meu amor, se eu precisasse escolher duas pessoas neste mundo, eu escolheria você e você.
Elemento inverso da adição lógica
0 + 1 = 1
1 + 0 = 1
Exemplo 1: O ladrão está sendo procurado vivo ou morto.
B = O ladrão ser procurado.
A = O ladrão estar vivo.
/A = O ladrão estar morto.
B = A + /A.
B = 1.
O ladrão será procurado.
Exercício 1: Você vai fazer o serviço, quer você queira, quer não.
Exercício 2: Você vai sair dessa cama por bem ou por mal.
Exercício 3: Fiat Moby, ou você tem, ou você não tem.
Elemento inverso da multiplicação lógica
0*1=0
1*0=0
Exemplo 1: Quero agradar a Deus e ao diabo.
B = Agradar.
A = A Deus.
/A = Ao diabo.
B = A * /A.
B = 0.
Não dá para agradar a ambos.
Exercício 1: Para que haja paz na selva, é preciso satisfazer a caças e a caçadores.
Exercício 2: Eu te amo, mas, ao mesmo tempo, eu te odeio.
Exercício 3: Utopia existencialista: Quero ser rico, mas luto por um mundo igualitário.
Elemento indiferente da adição lógica
0 + 0 = 0.
1 + 0 = 1.
Exemplo 1: Para que este projeto fracasse, só mesmo se o mercado financeiro entrar em crise ou se a Terra for invadida por alienígenas.
B = O projeto fracassar.
A = O mercado financeiro entrar em crise.
0 = A Terra ser invadida por alienígenas.
B = A+ 0.
B = A.
O projeto vai fracassar somente se o mercado financeiro entrar em crise.
Exercício 1: Eu vou pedir demissão somente se conseguir outro emprego melhor ou se ganhar na loteria.
Elemento indiferente da multiplicação lógica
0 * 1 = 0.
1 * 1 = 1
Exemplo 1: Para que este projeto funcione, basta que o mercado financeiro se recomponha e que o tempo passe.
B = O projeto funcionar.
A = O mercado financeiro se recompuser.
1 = O tempo passar.
B = A* 1.
B = A.
Basta que o mercado financeiro se recomponha.
Exercício 1: Para você passar na prova, basta estudar e ter um cérebro.
Elemento nulo da adição lógica
0 + 1 = 1
1 + 1 = 1
Exemplo: Para o momento desejado chegar, basta deixar o tempo passar, ou, então, distrair-se com outra coisa.
B = O momento desejado chegar.
A = Distrair-se com outra coisa.
1 = Deixar o tempo passar.
B = A+ 1.
B = 1.
O momento desejado vai chegar.
Elemento nulo da multiplicação lógica
0 * 0 = 0
1 * 0 = 0
Exemplo: Para permanecer jovem, basta cuidar da saúde e retardar o avanço do tempo.
B = Permanecer jovem.
A = Cuidar da saúde.
0 = Retardar o avanço do tempo.
B =A* 0.
B = 0.
Você não permanecerá jovem.
PROPRIEDADES
Propriedade Distributiva da multiplicação sobre a adição
(A * B) + (A * C) = A * (B + C)
Exemplo 1: Para o almoço, quero arroz com feijão ou arroz com lentilha. D = Almoço
A = Arroz
B = Feijão
C = Lentilha
D = (A * B) + (A * C)
D = A * (B + C)
Para o almoço, quero arroz com feijão ou com lentilha.
Exercício 1: A dança de formatura pode ser representada pelo João com a sua mãe ou pelo João com a sua esposa.
Propriedade Distributiva da adição sobre a multiplicação
(A + B) * (A + C) = A + (B * C)
Irrelevância
- Nem todas as combinações das variáveis de entrada precisam ser usadas.
- A decisão a ser tomada nas possibilidades que jamais acontecerão são irrelevantes.
Exemplo 1: Para o almoço, você escolhe carne ou massa, e, para sobremesa, você escolhe gelatina ou pudim.
E = A escolha
A = Carne
B = Massa
C = Gelatina
D = Pudim
E = (A + B) * (C + D)
Redução ao absurdo
0=1
Serve para encontrar: Absurdo, Mentira, Contradição, Incoerência, Inconsistência e Conflito.
Usado em situações como: Pais diante dos filhos, Patrão diante do empregado, Delegado diante do suspeito...
Exemplo 1: Queijo suíço: Este queijo tem o maior número de buracos.
- Quanto mais queijo, mais buracos.
- Se levarmos em consideração que os buracos ocupam o lugar onde deveria ter queijo, quanto mais buracos, menos queijo.
- Se quanto mais queijo mais buracos e quanto mais buracos menos queijo, logo quanto mais queijo, menos queijo.
A = Mais queijo 1. A = B
/A = Menos queijo 2. B = /A
B = Mais buracos 3. A = /A
O sistema é contraditório.
- A frase 1, ao afirmar que, quanto mais queijo, mais buracos, usa a palavra “queijo” para representar um todo que inclui os buracos.
- A fase dois, ao afirmar que os buracos ocupam o lugar onde deveria ter queijo, usa a palavra “queijo” para representar o não-buraco, e, neste caso, não seria o todo da frase um, mas, sim, a exclusão dos buracos.
- As frases 1 e 2 empregam um significado diferente para a mesma palavra, queijo, e, por isso, não podem ser usadas no mesmo argumento.
© Direitos de autor. 2020: Gomes; Sinésio Raimundo. Última atualização: 15/04/2020